C Locrian
C Locrian scale for guitar.
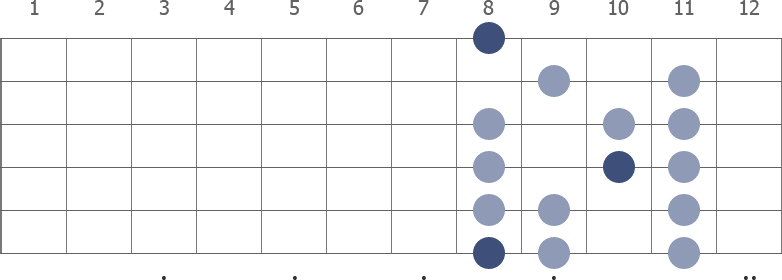
The C Locrian is a seven-note scale, it is also called a mode. Colored circles in the diagram mark the notes in the scale (darker color highlighting the root notes). In the fretboard pattern, the first root note is on the 6th string, 8th fret.
C Locrian 2 octaves
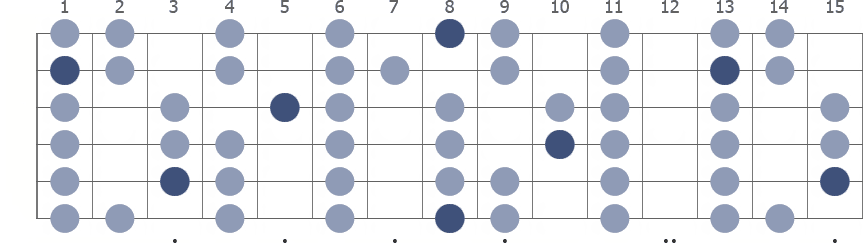
C Locrian full fretboard
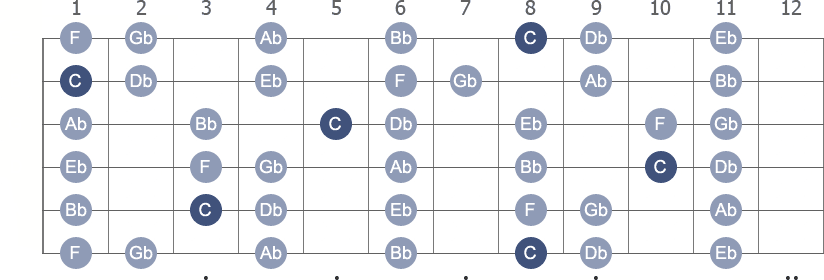
C Locrian note names
The scale displayed with its numeric formula, notes, intervals and scale degrees.
| Formula | Notes | Intervals | Degrees |
|---|---|---|---|
| 1 | C | Unison | Tonic |
| b2 | Db | Minor second | Supertonic |
| b3 | Eb | Minor third | Mediant |
| 4 | F | Perfect fourth | Subdominant |
| b5 | Gb | Diminished fifth | Dominant |
| b6 | Ab | Minor sixth | Submediant |
| b7 | Bb | Minor seventh | Subtonic |
The C Locrian scale consists of seven notes. These can be described as steps on the guitar fingerboard according to the following formula: half, whole, whole, half, whole, whole, whole from the first note to the same in the next octave.
The C Locrian is a mode of the Db Major Scale. It contains exactly the same notes, but starts on another note.
This scale is primarily used in jazz and is rare in popular music.
One way to learn this scale is to think of it as the Db Major starting from its seventh note. Another way is to think of it as the C Phrygian with a flattened 5th.
Chords that are related to this scale are the following:
| Cdim, Cm7b5 |
| Db, Dbmaj7, Db6, Db6/9, Dbmaj9, Dbmaj13 |
| Ebm, Ebm7, Ebm6, Ebm9, Ebm11, Ebm13 |
| Fm, Fm7 |
| Gb, Gbmaj7, Gb6, Gb6/9, Gbmaj9, Gbmaj13 |
| Ab, Ab7, Ab6, Ab6/9, Ab9, Ab11, Ab13 |
| Bbm, Bbm7, Bbm9, Bbm11 |
The tones in these chords correspond to the tones of the C Locrian scale.
Related to Locrian are Locrian ♮2 and Locrian #6, being the 4th mode of the Melodic Minor and the 2nd mode of the Harmonic Minor.
The C Locrian ♮2 scale, also called C Half-diminished scale, is identical with the C Locrian except for a major second instead of a minor second which is indicated by the natural symbol. It can be displayed as follows:
| Formula | Notes | Intervals | Degrees |
|---|---|---|---|
| 1 | C | Unison | Tonic |
| 2 | D | Major second | Supertonic |
| b3 | Eb | Minor third | Mediant |
| 4 | F | Perfect fourth | Subdominant |
| b5 | Gb | Diminished fifth | Dominant |
| b6 | Ab | Minor sixth | Submediant |
| b7 | Bb | Minor seventh | Subtonic |
The C Locrian ♮2 contains the same notes as the Eb Melodic Minor Scale, but starts on another note.
The C Locrian #6 scale is identical with the C Locrian except for a major sixth instead of a minor sixth which is indicated by the sharp symbol in the name. It can be displayed as follows:
| Formula | Notes | Intervals | Degrees |
|---|---|---|---|
| 1 | C | Unison | Tonic |
| b2 | Db | Minor second | Supertonic |
| b3 | Eb | Minor third | Mediant |
| 4 | F | Perfect fourth | Subdominant |
| b5 | Gb | Diminished fifth | Dominant |
| 6 | A | Major sixth | Submediant |
| b7 | Bb | Minor seventh | Subtonic |
The C Locrian #6 contains the same notes as the Bb Harmonic Minor Scale, but starts on another note.
Start the audio and play along with your guitar! Use notes from the scale in the diagram above.*
Normal tempo:Go to Jam Tracks section for more guitar jam tracks!
* In reality, Locrian scales are seldom used throughout a whole song.