F Minor
F Minor scale for guitar.
The F Minor is a seven-note scale, also called Natural F Minor. Colored circles mark the tones in the diagram, with darker color highlighting the root notes. The root notes are always F tones. In the two-octave pattern, the first root note is on the 6th string, 1st fret.
F Minor 2 octaves
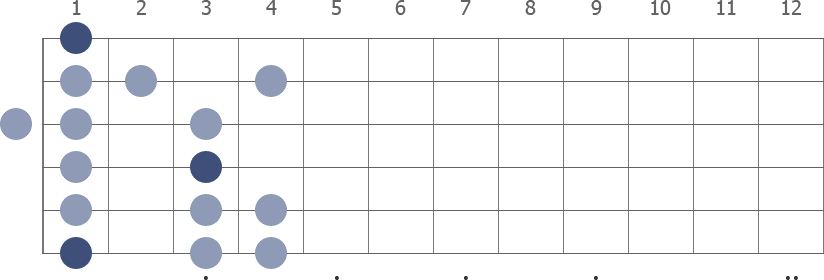
F Minor full fretboard
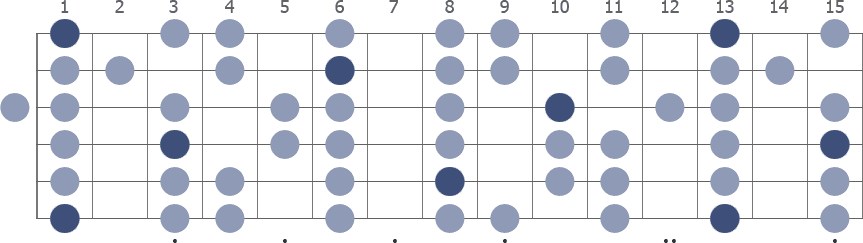
F Minor with note names
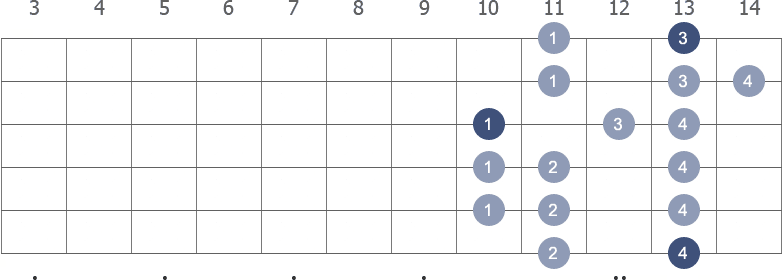
Shape 1 (12th position) with fingerings

Shape 2 (3rd position) with fingerings
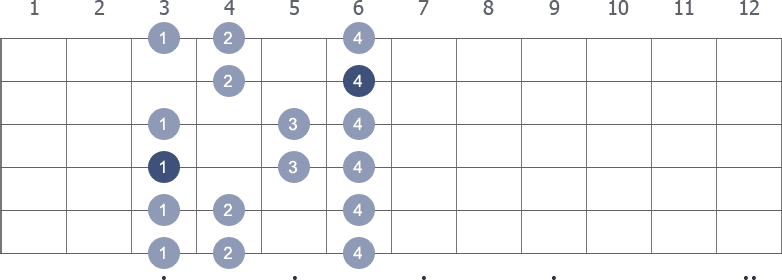
Shape 3 (5th position) with fingerings
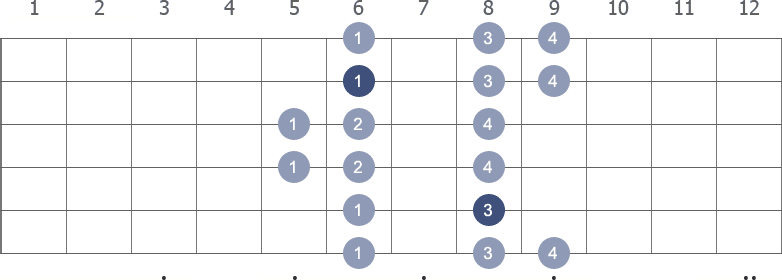
Shape 4 (8th position) with fingerings
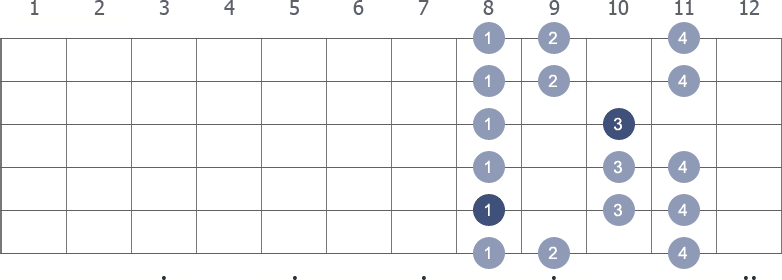
Shape 5 (10th position) with fingerings
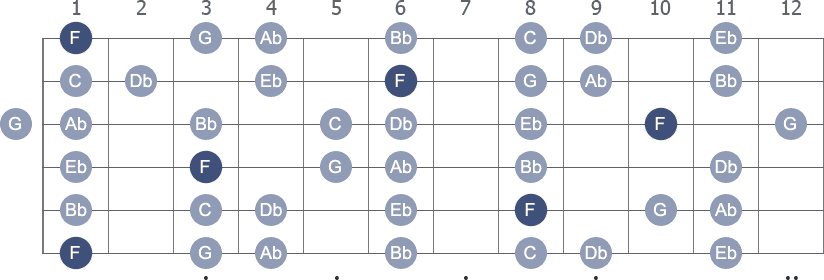
The scale displayed with its numeric formula, notes, intervals and scale degrees.
| Formula | Notes | Intervals | Degrees |
|---|---|---|---|
| 1 | F | Unison | Tonic |
| 2 | G | Major second | Supertonic |
| b3 | Ab | Minor third | Mediant |
| 4 | Bb | Perfect fourth | Subdominant |
| 5 | C | Perfect fifth | Dominant |
| b6 | Db | Minor sixth | Submediant |
| b7 | Eb | Minor seventh | Subtonic |
The interval formula (2 - 1 - 2 - 2 - 1 - 2 - 2) can be expound into specific notes of the scale.
| Notes (ascending) | Interval |
|---|---|
| F-G | M2 |
| F-Ab | m3 |
| F-Bb | P4 |
| F-C | P5 |
| F-Db | m6 |
| F-Eb | m7 |
| Notes (descending) | Interval |
|---|---|
| F-Eb | M2 |
| F-Db | M3 |
| F-C | P4 |
| F-Bb | P5 |
| F-Ab | M6 |
| F-G | m7 |
Abbreviations are used: M / m stands for major / minor and P stands for perfect.
The F Minor scale consists of seven notes. These can be described as intervals, as semi-notes or steps on the guitar fingerboard, written as 2 - 1 - 2 - 2 - 1 - 2 - 2 from the first note to the next octave.
The F Minor is relative to Ab Major. Both scales include the same notes but their tonal center differ.
The F Minor is identical with the F Aeolian mode.
Beneficial to learn this scale is to observe the note steps starting from the root: whole, half, whole, whole, half, whole, whole. The same formula applies for the whole neck.
These are chords built from the notes of this scale:
| Fm, Fm7, Fm9, Fm11 |
| Gdim, Gm7b5 |
| Ab, Abmaj7, Ab6, Ab6/9, Abmaj9, Abmaj13 |
| Bbm, Bbm7, Bbm6, Bbm9, Bbm11, Bbm13 |
| Cm, Cm7 |
| Db, Dbmaj7, Db6, Db6/9, Dbmaj9 |
| Eb, Eb7, Eb6, Eb9, Eb11, Eb13 |
The tones in these chords correspond to the tones of the F Minor scale in which Fm is the tonic triad and Fm7 the tonic 7th chord.
Start the audio and play along with your guitar! Use notes from the scale in the diagram above.
Normal tempo:F Minor scale first shape ascending.
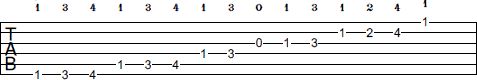
The numbers above the tablature are suggested fingerings.