D# Major
D sharp Major scale for guitar.
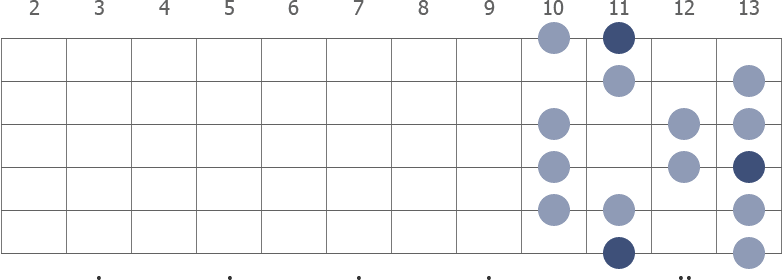
The D# Major is a seven-note scale. Notes are displayed in the diagram with blue color with the root notes indicated by darker color. The root notes are always D# tones. In the two-octave pattern, the first root note is on the 6th string, 11th fret.
D# Major 2 octaves
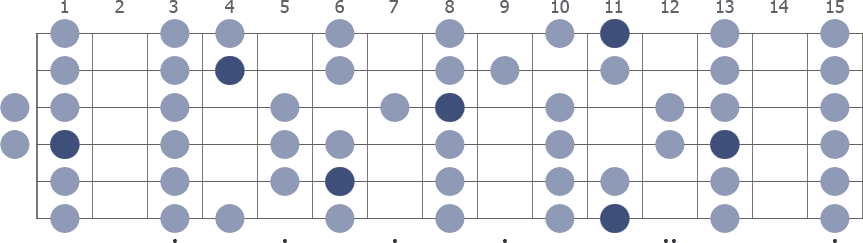
D# Major full fretboard
D# Major note names

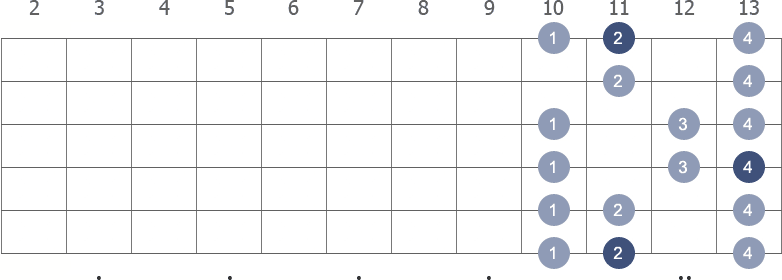
Shape 1 (10th position) with fingerings
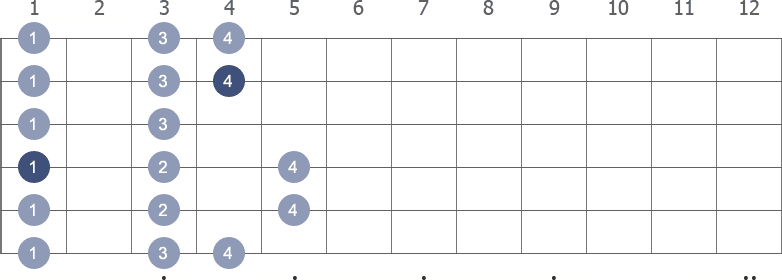
Shape 2 (1st position) with fingerings
Shape 3 (3rd position) with fingerings
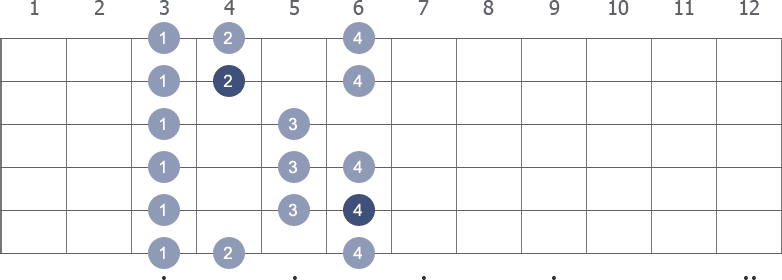
Shape 4 (5th position) with fingerings
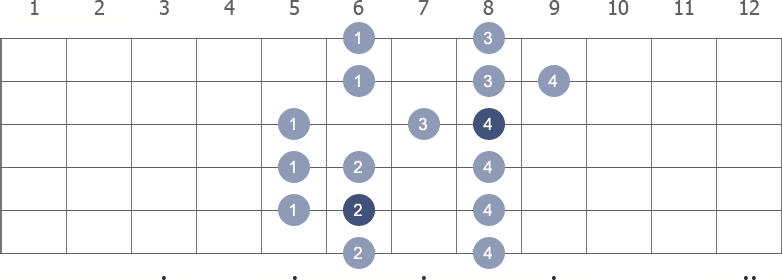
Shape 5 (7th position) with fingerings
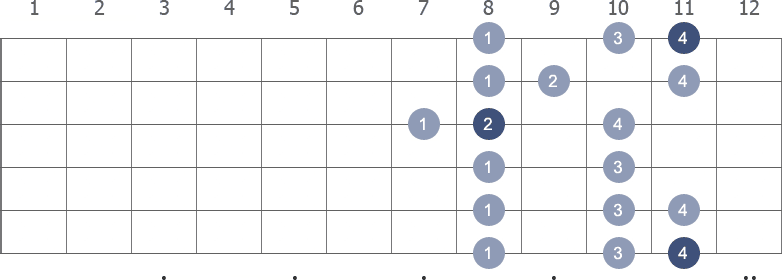
Root on 5th string
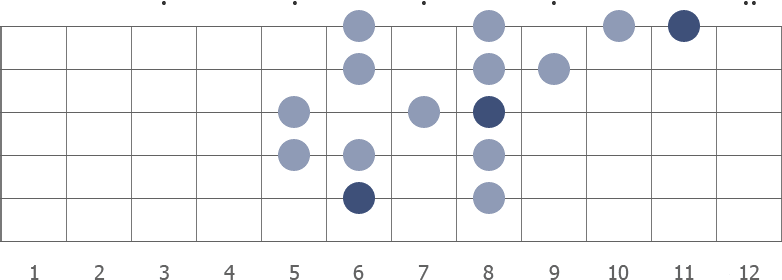
The scale displayed with its numeric formula and scale degrees.
| Formula | Notes | Intervals | Degrees |
|---|---|---|---|
| 1 | D# | Unison | Tonic |
| 2 | E# | Major second | Supertonic |
| 3 | F## | Major third | Mediant |
| 4 | G# | Perfect fourth | Subdominant |
| 5 | A# | Perfect fifth | Dominant |
| 6 | B# | Sixth | Submediant |
| 7 | C## | Major seventh | Leading tone |
The second degree is written as E#, which is the same as F. The third degree is written as F##, which is the same as G. The sixth degree is written as B#, which is the same as C. The seventh degree is written as C##, which is the same as D. A practice in a scale notation is to not include the same letter twice, if it can be avoided.
The interval formula (2 - 2 - 1 - 2 - 2 - 2 - 1) can be expound into specific notes of the scale.
| Notes (ascending) | Interval |
|---|---|
| D#-F | M2 |
| D#-G | M3 |
| D#-G# | P4 |
| D#-A# | P5 |
| D#-C | M6 |
| D#-D | M7 |
| Notes (descending) | Interval |
|---|---|
| D#-D | m2 |
| D#-C | m3 |
| D#-A# | P4 |
| D#-G# | P5 |
| D#-G | m6 |
| D#-F | m7 |
Abbreviations are used: M / m stands for major / minor and P stands for perfect.
The main three-note and four-note chords that are related to this scale are the following:
| Chord | Fingering | Chord | Fingering |
|---|---|---|---|
| D# | X68886 | D#maj7 | X68786 |
| Fm | 133111 | Fm7 | 131111 |
| Gm | 355333 | Gm7 | 353333 |
| G# | 466544 | G#maj7 | 465544 |
| A# | X13331 | A#7 | X13131 |
| Cm | X35543 | Cm7 | X35343 |
| Ddim | X5676X | Dm7b5 | X5656X |
The tones in these chords correspond to the tones of the D# Major scale in which D# is the tonic triad and D#maj7 the tonic 7th chord.
The second and fourth columns include short notations for the chords in the first and third columns respectively. These are based on common ways to play the chord, but there are other alternatives. See more about this notation system on the FAQ page.
The D sharp Major consists of seven notes (D# - E# - F## - G# - A# - B# - C##). These can be described as intervals, as semi-notes or steps on the guitar fingerboard, written as 2 - 2 - 1 - 2 - 2 - 2 - 1 from the first note to the next octave.
The scale can be played on the guitar from different starting positions in which D# functions as the tonic.
The D# Major is relative to C Minor, which means that both scales include the same notes but with different tonal center.
The D# Major is identical with the D# Ionian mode.
The D sharp Major scale has three raised notes: D# (D sharp), G# (G sharp) and A# (A sharp). Noticing these notes is one of the ways to memorize the scale.
Start the audio and play along with your guitar! Use notes from the scale in the diagram above.
Normal tempo:The D sharp scale presented in sheet music notation.

The sheet music includes two octaves played ascending and descending. The E flat key signature is commonly used instead of D sharp (the key signature of D sharp includes double sharps).